Mari pelajari contoh kasus ini untuk eksplorasi kreativitas kita!
Sebuah Pengantar:
Artikel ini menyajikan sebuah eksplorasi matematika yang berfokus pada sesuatu yang tampak sederhana: operasi pembagian. Pembagian adalah salah satu operasi dasar dalam matematika, bersama dengan penjumlahan, pengurangan, dan perkalian, yang biasanya diperkenalkan di bangku sekolah dasar. Namun, metode yang umum kita gunakan sering kali dianggap sebagai prosedur baku—memberikan kesan bahwa ini satu-satunya cara yang pasti untuk menyelesaikan permasalahan ini.
Bayangkan jika peserta didik di sekolah percaya bahwa hanya ada satu cara untuk melakukan pembagian. Padahal, pendidikan seharusnya membuka kemungkinan baru, memicu pertanyaan, mendorong rasa ingin tahu, dan menginspirasi siswa untuk menikmati perjalanan belajar yang penuh dengan eksplorasi. Itulah mengapa kita akan mencoba pendekatan yang sedikit berbeda—metode yang secara tidak sengaja saya temukan ketika masih duduk di bangku SMP.
Sebagian besar dari kita tentu sudah akrab dengan metode pembagian panjang. Melalui artikel ini, kita akan menjelajahi pembagian dari sudut pandang yang berbeda—sebuah metode yang tidak konvensional dan tidak dimaksudkan untuk menggantikan pendekatan standar yang diajarkan di sekolah. Sebaliknya, metode ini merupakan bagian dari eksplorasi matematika yang membuka wawasan akan kemungkinan-kemungkinan lain di luar yang sudah kita kenal.
Mari kita mulai dengan contoh menggunakan metode konvensional terlebih dahulu!
Contoh Problem: Metode Pertama



Metode yang baru saja digunakan adalah metode yang umum kita gunakan dalam pembelajaran matematika.
Contoh Problem: Metode Kedua
Sekarang, mari kita beralih ke pendekatan yang pernah saya coba—mungkin terasa sedikit berlawanan dengan intuisi pada awalnya.
Sama seperti sebelumnya, kita membagi 45 dengan 23. Namun kali ini, saya akan mencoba menggunakan 2 sebagai hasil bagi, yang menghasilkan 46. Mengapa saya memilih 2? Karena 46 lebih mendekati 45.

Apa masalahnya jika sisanya negatif? Bilangan negatif memang bisa terasa rumit jika dihubungkan dengan objek-objek “nyata” dalam kehidupan sehari-hari, tetapi dalam matematika, bilangan negatif sepenuhnya valid dan dapat dipahami dengan perspektif yang tepat. Itulah alasan saya tetap menggunakan metode ini—meskipun menghasilkan sisa negatif. Kita akan melihat bahwa pendekatan ini meberikan hasil yang lebih sederhana.
Sekarang, kita “turunkan” angka 9, yang berarti kita harus menempatkan angka 0 di atasnya dalam hasil bagi. Ingat, angka yang diturunkan dari soal “ditambahkan” ke sisa sebelumnya. Ini menghasilkan hasil berikut:
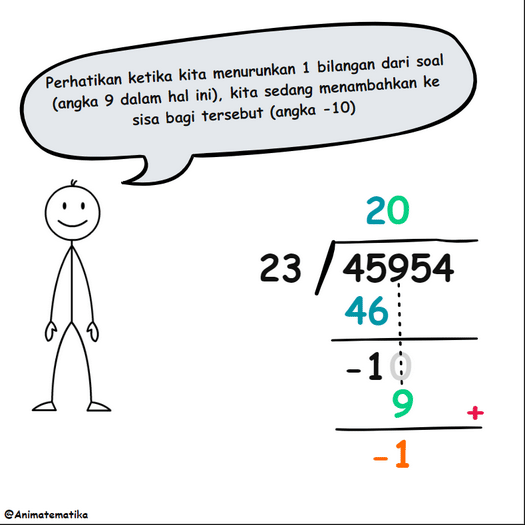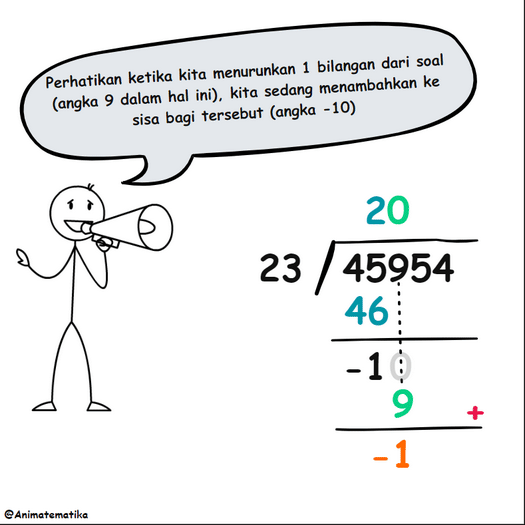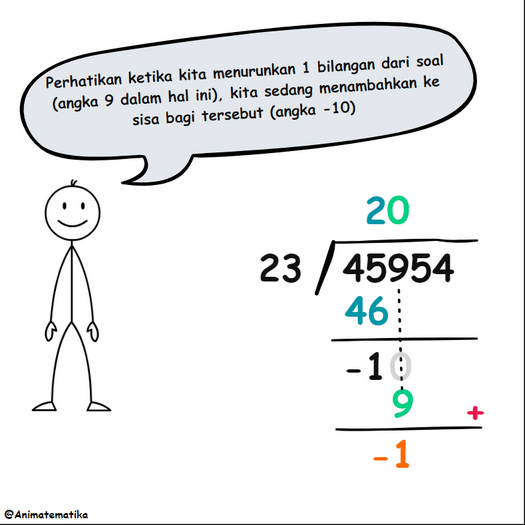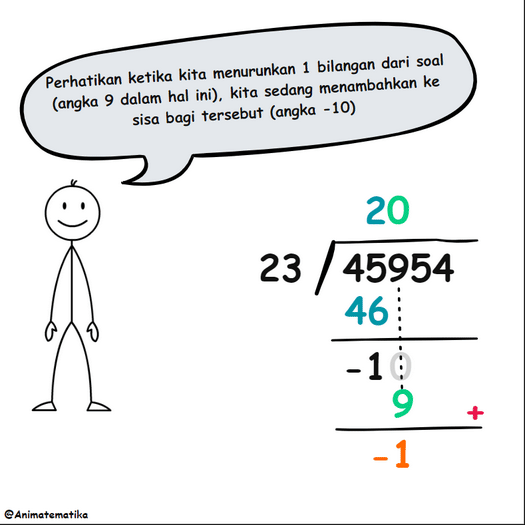
Namun, kita bisa menurunkan semua digit dari soal sekaligus, dan cara ini tampaknya lebih efisien. Dengan menuliskan 000 pada hasil bagi, ketiga digit dari soal diturunkan secara bersamaan, menghasilkan proses berikut:
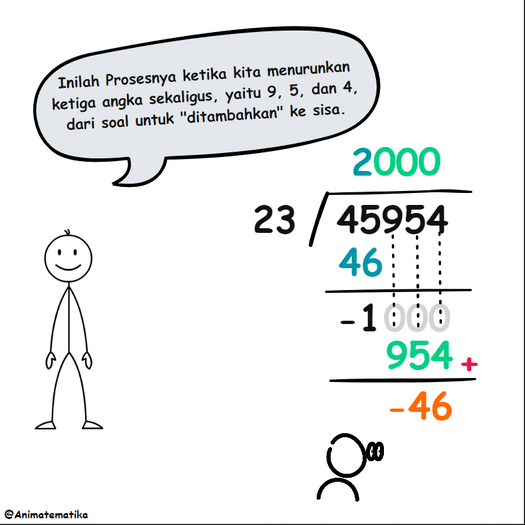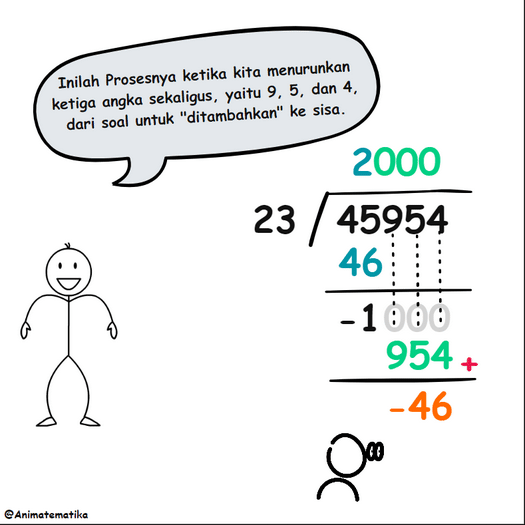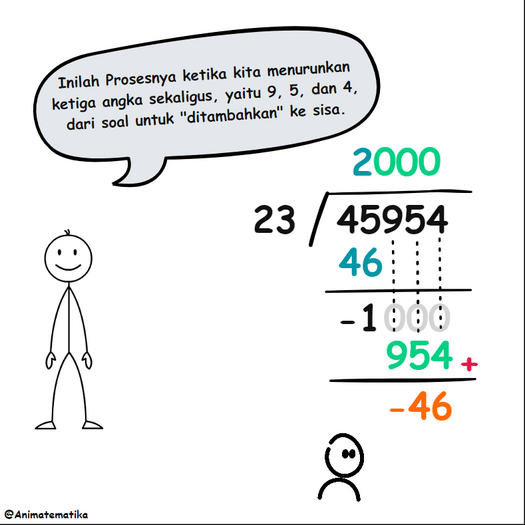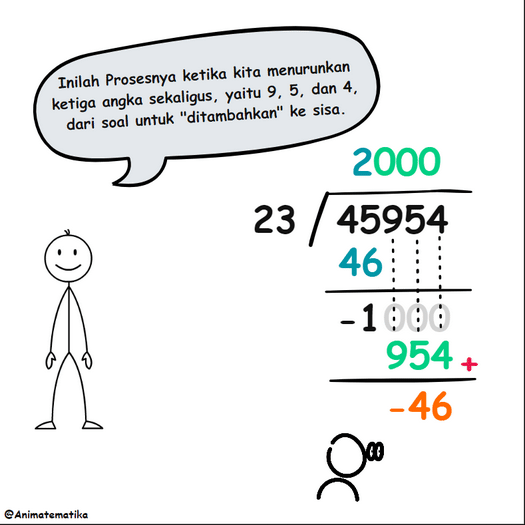
Perhatikan bahwa ketika 954 diturunkan dan ditambahkan ke -1, sebenarnya kita menambahkannya ke -1000, karena angka nol tersebut secara implisit ada meskipun tidak tertulis. Jadi, perhitungannya menjadi -1000 ditambah 954, yang menghasilkan -46.
Untuk menghilangkan sisa -46, kita menggunakan hasil bagi -2, karena -2 dikalikan dengan 23 menghasilkan -46. Ini akan menghilangkan -46 dari sisa sebelumnya, menguranginya menjadi nol. Proses ini menghasilkan bentuk berikut:

Jadi, kita mendapatkan hasil bagi sebesar 2000 – 2, yang sama dengan 1998.
Jika kita membandingkan metode konvensional dengan pendekatan baru yang baru saja dilakukan, kita akan melihat perbandingan berikut:
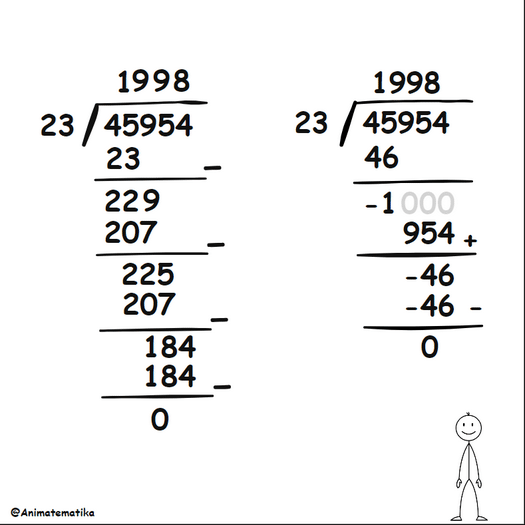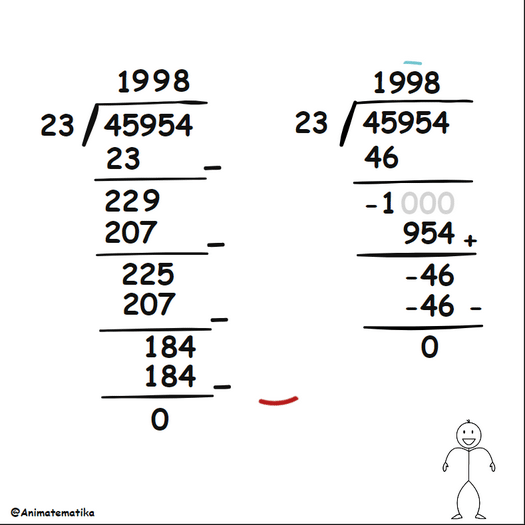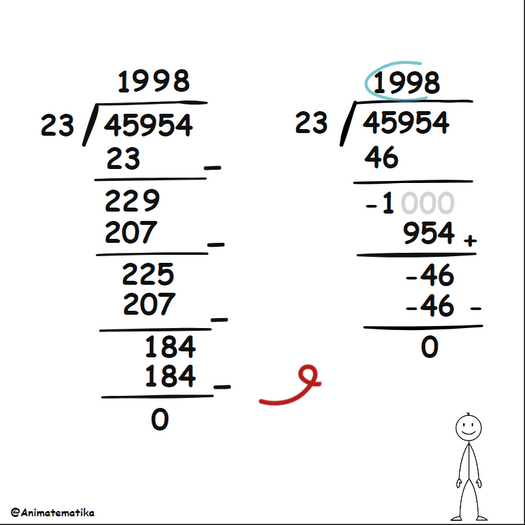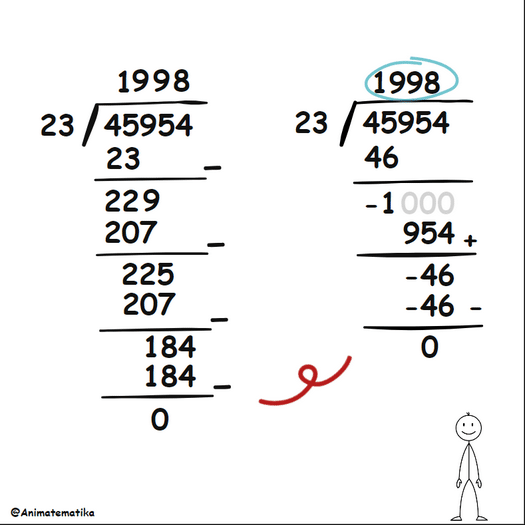
Perhatikan bahwa metode di sebelah kanan sebenarnya lebih singkat dalam hal prosedur! Dengan demikian kita dapat mengatakan bahwa metode yang kanan ini lebih efisien. Namun, ini mungkin menimbulkan beberapa pertanyaan: Bagaimana jika sisanya tidak nol? Bagaimana jika hasil baginya berupa desimal? Bukankah metode ini justru bisa memperumit jika angka pada soalnya berbeda?
Metode ini memang tidak dirancang untuk menangani skenario yang lebih kompleks seperti itu. Sekali lagi, inti dari metode ini adalah eksplorasi, bukan untuk mencari metode paling termuktakhir untuk segala persoalan.
Apakah kita bersedia keluar dari zona nyaman dan mencoba pendekatan berbeda untuk menyelesaikan suatu masalah? Sering kali, prosedur yang sudah kita kenal membuat kita merasa nyaman, dan kita ragu untuk mencoba sesuatu yang baru. Namun, bukankah pemecahan masalah, keasyikan dalam menemukan hal baru, dan rasa ingin tahu yang kita kembangkan semua berakar pada kesediaan kita untuk melangkah ke wilayah yang belum terjelajah?
Keberanian untuk keluar dari prosedur umum sering kali memicu inovasi. Isaac Newton, dalam karyanya tentang ekspansi binomial, berani melangkah lebih jauh dengan mengeksplorasi eksponen di luar bilangan bulat positif. Ia menggantikan n=−1 ke dalam:
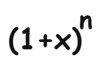
Ketika dianalisis secara matematis, persaman tersebut menghasilkan deret tak hingga. Penemuan Newton tidak hanya mengungkapkan deret ini, tetapi juga mendorong perkembangan studi tentang deret tak hingga ke tingkat yang lebih tinggi.
Sekarang, Anda juga bisa mencobanya. Saya akan memberikan sebuah soal yang bisa Anda gunakan untuk berlatih dengan metode “tidak biasa” ini. Berikan diri Anda ruang untuk berkreasi—karena inilah yang menumbuhkan kreativitas.
Tantangan: Coba gunakan metode ini untuk menyelesaikan pembagian 50983 ÷ 17!
Sebagai rangkuman dari pembahasan kita, saya telah membuat video animasi khusus untuk Anda. Semoga Anda menyukainya! Agar lebih menarik, cobalah untuk mengaktifkan fitur audio juga. Berikut animasinya:
Bagi yang tertarik dengan artikel ini dalam bahasa Inggris, silahkan akses tulisan di bawah ini:
Reimagining Simple Division: A Bold Exploration Beyond Convention
Have you ever taken a moment to reflect and ponder whether the way you’ve been doing division is really the only way? or Maybe there are simpler and more exciting methods beyond the rigid procedures drilled into you at school. Isn’t the courage to try new things at the very heart of learning, especially when we’re in the midst of exploration? Perhaps now’s the time to venture off the familiar path — to rediscover the thrill that lies at the heart of doing mathematics.